Em matemática, denomina-se interpolação
o método que permite construir um novo conjunto de dados a partir de um
conjunto discreto de dados pontuais previamente conhecidos.
Em engenharia e ciência, dispõe-se habitualmente de dados pontuais obtidos a partir de uma amostragem ou de um experimento. Tal conjunto de dados pontuais (também denominado conjunto degenerado) não possui continuidade, e isto muitas vezes torna demasiado irreal a representação teórica de um fenômeno real empiricamente observado.
Através da interpolação, pode-se construir uma função que aproximadamente se "encaixe" nestes dados pontuais, conferindo-lhes, então, a continuidade desejada.
Outra aplicação da interpolação é a aproximação de funções complexas
por funções mais simples. Suponha que tenhamos uma função, mas que seja
complicada demais para que seja possível avaliá-la de forma eficiente.
Podemos, então, escolher alguns dados pontuais da função complicada e
tentar interpolá-los com uma função mais simples. Obviamente, quando
utilizamos a função mais simples para calcular novos dados, normalmente
não se obtém o mesmo resultado da função original, mas dependendo do
domínio do problema e do método de interpolação utilizado, o ganho de
simplicidade pode compensar o erro.
A interpolação permite fazer a reconstituição (aproximada) de uma
função, bastando para tanto conhecer apenas algumas das suas abscissas e
respectivas ordenadas (imagens no contra-domínio da função). A função
resultante garantidamente passa pelos pontos fornecidos, e, em relação
aos outros pontos, pode ser considerada um mero ajuste.
 |
| Exemplo de interpolação linear |
 |
| Exemplo de interpolação polinomial de grau superior a 1 |
Tipos de interpolação
- Interpolação linear
- Interpolação polinomial
- Interpolação trigonométrica
Interpolação linear
Definição
Em matemática, denomina-se interpolação linear o método de interpolação que se utiliza de uma função linear p(x) (um polinômio de primeiro grau) para representar, por aproximação, uma suposta função f(x) que originalmente representaria as imagens de um intervalo descontínuo (ou degenerado) contido no domínio de f(x).
Assim sendo, se aquele intervalo for, por exemplo, o intervalo das abscissas 
 , e
, e 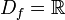 (
(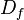 é o domínio da função f(x)), o que a definição diz é que todos os elementos de
é o domínio da função f(x)), o que a definição diz é que todos os elementos de  estão em
estão em  , mas nem todos
, mas nem todos  estão em
estão em  e por esta razão
e por esta razão  se diz um intervalo descontínuo ou degenerado, sendo necessário usar uma função p(x) para compensar a descontinuidade de f(x) naquele intervalo de abscissas.
se diz um intervalo descontínuo ou degenerado, sendo necessário usar uma função p(x) para compensar a descontinuidade de f(x) naquele intervalo de abscissas.

 , e
, e 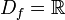 (
(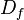 é o domínio da função f(x)), o que a definição diz é que todos os elementos de
é o domínio da função f(x)), o que a definição diz é que todos os elementos de  estão em
estão em  , mas nem todos
, mas nem todos  estão em
estão em  e por esta razão
e por esta razão  se diz um intervalo descontínuo ou degenerado, sendo necessário usar uma função p(x) para compensar a descontinuidade de f(x) naquele intervalo de abscissas.
se diz um intervalo descontínuo ou degenerado, sendo necessário usar uma função p(x) para compensar a descontinuidade de f(x) naquele intervalo de abscissas.
Em outras palavras: quando se dispõe somente do intervalo 
 e dos valores
e dos valores 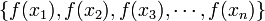 , sem se conhecer a expressão matemática da função f(x), pode-se aplicar o polinômio interpolador de primeiro grau p(x) para que se tenha uma função contínua em
, sem se conhecer a expressão matemática da função f(x), pode-se aplicar o polinômio interpolador de primeiro grau p(x) para que se tenha uma função contínua em ![[x_{1};x_{n}]](http://upload.wikimedia.org/math/1/b/b/1bb88351f69fc89d370ddf74e37de1c7.png) (
( ) e, conseqüentemente, com suas abscissas interceptando todos os elementos de
) e, conseqüentemente, com suas abscissas interceptando todos os elementos de  (
(![\ne [x_{1};x_{n}]](http://upload.wikimedia.org/math/1/1/5/115689e0d7c79ad3a1f3d514e8d888d7.png) ).
).

 e dos valores
e dos valores 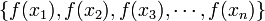 , sem se conhecer a expressão matemática da função f(x), pode-se aplicar o polinômio interpolador de primeiro grau p(x) para que se tenha uma função contínua em
, sem se conhecer a expressão matemática da função f(x), pode-se aplicar o polinômio interpolador de primeiro grau p(x) para que se tenha uma função contínua em ![[x_{1};x_{n}]](http://upload.wikimedia.org/math/1/b/b/1bb88351f69fc89d370ddf74e37de1c7.png) (
( ) e, conseqüentemente, com suas abscissas interceptando todos os elementos de
) e, conseqüentemente, com suas abscissas interceptando todos os elementos de  (
(![\ne [x_{1};x_{n}]](http://upload.wikimedia.org/math/1/1/5/115689e0d7c79ad3a1f3d514e8d888d7.png) ).
).
O principal problema é que se os pontos forem poucos ou muito
afastados entre si, a representação gráfica para uma determinada função
não seria muito bem representada por tal método. Neste caso, costuma-se
utilizar polinômios de graus mais elevados ou aplicar outros métodos. Um
deles é o método de Lagrange.
Interpolação polinomial
Definição
Denomina-se interpolação polinomial o processo matemático de interpolação em que a função interpoladora é um polinômio. A função interpoladora é a função 

Definidos um intervalo ![[a;b] \sub \mathbb{R}](http://upload.wikimedia.org/math/0/1/0/0100474d708e6f9914c22dcb584080b7.png) e uma função
e uma função ![f:[a;b] \rightarrow \mathbb{R},](http://upload.wikimedia.org/math/3/4/3/343e1b84f1b7625100b8961234f0c929.png) denomina-se interpolação o processo matemático de avaliar
denomina-se interpolação o processo matemático de avaliar ![f(x), \forall x \in [a;b],](http://upload.wikimedia.org/math/b/1/b/b1b1bab043442676d754c5b0c7ab6b9c.png) substituindo-se a função
substituindo-se a função  pela função interpoladora
pela função interpoladora  de modo que
de modo que ![p(x_i)=f(x_i), \forall i \in [1;n]](http://upload.wikimedia.org/math/b/e/5/be57250651aebbd59a196023128e4880.png) (
( ).
).
![[a;b] \sub \mathbb{R}](http://upload.wikimedia.org/math/0/1/0/0100474d708e6f9914c22dcb584080b7.png) e uma função
e uma função ![f:[a;b] \rightarrow \mathbb{R},](http://upload.wikimedia.org/math/3/4/3/343e1b84f1b7625100b8961234f0c929.png) denomina-se interpolação o processo matemático de avaliar
denomina-se interpolação o processo matemático de avaliar ![f(x), \forall x \in [a;b],](http://upload.wikimedia.org/math/b/1/b/b1b1bab043442676d754c5b0c7ab6b9c.png) substituindo-se a função
substituindo-se a função  pela função interpoladora
pela função interpoladora  de modo que
de modo que ![p(x_i)=f(x_i), \forall i \in [1;n]](http://upload.wikimedia.org/math/b/e/5/be57250651aebbd59a196023128e4880.png) (
( ).
).
Assim,  é a função real, definida em
é a função real, definida em ![[a;b] \sub \mathbb{R},](http://upload.wikimedia.org/math/d/2/f/d2fff517ce8ed17b6db8178d099fe1e1.png) da qual conhecem-se os valores nos pontos de abcissas
da qual conhecem-se os valores nos pontos de abcissas ![x_1, x_2, x_3,..., x_i \in [a;b], \forall i \in [1;n]](http://upload.wikimedia.org/math/f/8/0/f80e54063b80774b9f368911dd5d0a5e.png) (
( ).
).
 é a função real, definida em
é a função real, definida em ![[a;b] \sub \mathbb{R},](http://upload.wikimedia.org/math/d/2/f/d2fff517ce8ed17b6db8178d099fe1e1.png) da qual conhecem-se os valores nos pontos de abcissas
da qual conhecem-se os valores nos pontos de abcissas ![x_1, x_2, x_3,..., x_i \in [a;b], \forall i \in [1;n]](http://upload.wikimedia.org/math/f/8/0/f80e54063b80774b9f368911dd5d0a5e.png) (
( ).
).
Na fase de escolha do processo matemático de interpolação,
frequentemente são escolhidos polinómios. Isto porque os polinómios
apresentam relativa simplicidade, e também porque permitem representar
satisfatoriamente a generalidade das funções que surgem no dia-a-dia.
Métodos de interpolação polinomial
Os métodos de interpolação polinomial diferem, uns dos outros, quanto
à técnica de determinação do polinómio interpolador. Os erros de
arredondamento diferem em cada caso, pois as operações aritméticas são
conduzidas de formas distintas, em cada método.
- Método de Newton
- Método de Lagrange
- Método de Bernstein
Exemplo
Quer-se achar o polinômio do terceiro grau que interpola a tabela:
x f(x)
1 -17
2 4
3 71
4 202
Constroe-se o sistema A.X = B
A =
1 1 1 1
1 2 4 8
1 3 9 27
1 4 16 64
Em A, a segunda coluna são os valores de x, a terceira coluna é a segunda ao quadrado e a quarta é a segunda ao cubo.
B =
-17
4
71
202
As raízes deste sistema são os coeficientes do polinômio:
X =
-10
-15
5
3
f(x)=3x³+5x²-15x-10
Interpolação trigonométrica
Em matemática, interpolação trigonométrica é processo pelo qual se obtém um polinômio trigonométrico que passa por um conjunto de pares (x,y) dados. É uma forma de interpolação adequada somente para funções periódicas.
Índice
- 1 Formulação do Problema
- 2 Formulação no plano complexo
- 3 Exemplos
- 3.1 Exemplo 1
- 3.1.1 Exemplo 2
- 3.1 Exemplo 1
Formulação do Problema
O polinômio trigonométrico de grau n tem a forma:
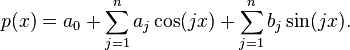
com 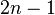 coeficientes:
coeficientes: 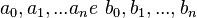 . Todo problema de interpolação é descrito como
. Todo problema de interpolação é descrito como
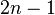 coeficientes:
coeficientes: 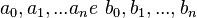 . Todo problema de interpolação é descrito como
. Todo problema de interpolação é descrito como
, onde  . Como o polinômio trigonométrico tem período
. Como o polinômio trigonométrico tem período 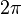 , podemos assumir que
, podemos assumir que 
 . Como o polinômio trigonométrico tem período
. Como o polinômio trigonométrico tem período 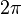 , podemos assumir que
, podemos assumir que 
O problema agora é encontrar coeficientes, de forma que o polinômio trigonométrico satisfaça as condições de interpolação.
Se o número de pontos for ímpar: 
e![\Psi(x)= \frac{A _{0} }{2}+ \sum_{k=1}^{m}[A _{k} \cdot \cos(k \cdot x)+B _{k} \cdot \sin(k \cdot x) ]](http://upload.wikimedia.org/math/2/c/a/2ca99378bd414d7155ce2a668d36fafb.png)
Se o número de pontos for par:
e![\Psi(x)= \frac{A _{0} }{2}+ \sum_{k=1}^{m-1}[A _{k} \cdot \cos(k \cdot x)+B _{k} \cdot \sin(k \cdot x) ]+ \frac{A _{m} }{2} \cdot \cos(m \cdot x)](http://upload.wikimedia.org/math/4/7/3/4733605899a32767e79179d7564c4879.png)
Para ambos os casos:

e
![\Psi(x)= \frac{A _{0} }{2}+ \sum_{k=1}^{m}[A _{k} \cdot \cos(k \cdot x)+B _{k} \cdot \sin(k \cdot x) ]](http://upload.wikimedia.org/math/2/c/a/2ca99378bd414d7155ce2a668d36fafb.png)
Se o número de pontos for par:

e
![\Psi(x)= \frac{A _{0} }{2}+ \sum_{k=1}^{m-1}[A _{k} \cdot \cos(k \cdot x)+B _{k} \cdot \sin(k \cdot x) ]+ \frac{A _{m} }{2} \cdot \cos(m \cdot x)](http://upload.wikimedia.org/math/4/7/3/4733605899a32767e79179d7564c4879.png)
Para ambos os casos:
Formulação no plano complexo
Utilizando a fórmula de De Moivre, podemos reescrever a soma de seno e cosseno como
 Então o polinômio pode ser escrito como
Então o polinômio pode ser escrito como
 Então o polinômio pode ser escrito como
Então o polinômio pode ser escrito como
onde  ,
,  e
e 
Se podemos reescrever
podemos reescrever 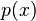 como
como 
onde é um polinômio de grau
é um polinômio de grau 
O problema de interpolação, então, resume-se a
 ,
,  e
e 
Se
 podemos reescrever
podemos reescrever 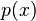 como
como 
onde
 é um polinômio de grau
é um polinômio de grau 
O problema de interpolação, então, resume-se a

Exemplos
Exemplo 1
Encontrar o polinômio interpolador trigonométrico de grau dois para  em
em ![[0;2]](http://upload.wikimedia.org/math/7/a/6/7a6df794fbd855c933275991bed807e4.png)

de forma que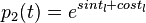 e
e  onde
onde 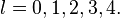



 em
em ![[0;2]](http://upload.wikimedia.org/math/7/a/6/7a6df794fbd855c933275991bed807e4.png)

de forma que
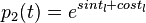 e
e  onde
onde 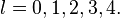



Exemplo 2
Interpolar os seguintes pontos:
Número de pontos
 (par) Grau:
(par) Grau: 
- Resultado:
![A _{j}= \frac{2}{n} \sum_{k=0}^{n-1}[f(x _{k}) \cdot \cos(j \cdot x _{k} ) ]](http://upload.wikimedia.org/math/a/c/7/ac7a3eac69bbd410ea1e89b8e136e865.png)
![B _{j}= \frac{2}{n} \sum_{k=0}^{n-1}[f(x _{k}) \cdot \sin(j \cdot x _{k} ) ]](http://upload.wikimedia.org/math/9/3/2/932cded2c67fd5bd2cdb4c915f406a44.png)



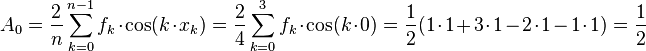
![A_1=\frac{2}{4} \sum\limits_{k=0}^{3}f_k\cdot \cos(k\cdot x_k)= \frac{1}{2}[1\cdot \cos(0)+3\cdot \cos(\frac{\pi}{2})-2\cdot \cos(\pi)-1\cdot \cos(\frac{3}{2}\pi)]=\frac{3}{2}](http://upload.wikimedia.org/math/1/e/0/1e0fdc4d54e5bb8e4eaa64dc85f226dc.png)
![A_2=\frac{2}{4} \sum\limits_{k=0}^{3}f_k\cdot \cos(k\cdot x_k)= \frac{1}{2}[1\cdot \cos(0)+3\cdot \cos(\pi)-2\cdot \cos(2\pi)-1\cdot \cos(3\pi)]=-\frac{3}{2}](http://upload.wikimedia.org/math/8/b/1/8b117f28145f0a78471c2b26660516dd.png)

![B_1=\frac{2}{4} \sum\limits_{k=0}^{n-1}f_k\cdot \sin(k\cdot x_k)= \frac{1}{2}[1\cdot 0+3\cdot 1-2\cdot 0-1\cdot (-1)]=2](http://upload.wikimedia.org/math/5/c/a/5ca218fae71072fd48e2044ecf3bdc99.png)


Sem comentários:
Enviar um comentário